Convex Hull - Part 2
先来说两个简单的计算几何小问题:
给定两个二维线段,判定它们是否相交?
当然最笨的办法就是求出两个线段方程,判断解是否满足要求。但这会引入除法操作,这不是我们希望的结果。
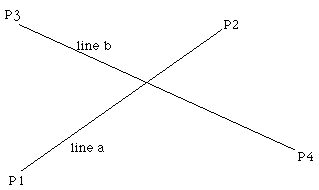
如上图,考虑 是否在线段 的异侧(toLeft 返回值不同则表示在异侧)。当然只做这一次异侧判断是不行的,对称地考虑 是否在线段 的异侧。如果两次异侧判断都成功,则说明两个线段相交。这种方法只需要进行 次 toLeft 判断,提高了效率。
用极点法求出若干极点后,如何将其排成环?
假设 leftmost-then-lowest 的极点为 ,定义 。按照上述定义的偏序关系就可以对所有极点排序,排序后从小到大即可。
从上面两道小题能够看出 toLeft 判定的重要性,这个判定函数将会贯穿计算几何的学习历程。
极边法(Extreme Edges)
从极点法我们可以自然而然地想到,如果遍历点集中所有可能成为凸包边界(极边)的线段,也能达到求解凸包的目的。事实上,我们也只需要对点集中每两个点相连的线段判断其余点是否都处于它的一侧即可。
所以极边法的时间复杂度相对极点法要低一些,遍历所有线段() 个 toLeft 判断 的复杂度,虽然好一些但还不够。
增量法(Incremental Construction)
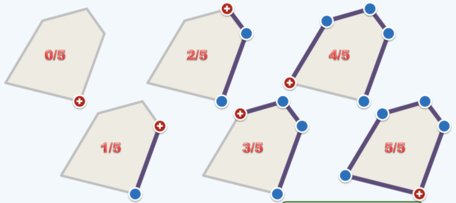
顾名思义,增量法的主要思路就是遍历点集中的所有点,每次都更新当前已遍历点集的凸包,最后得到对于所有点的凸包。
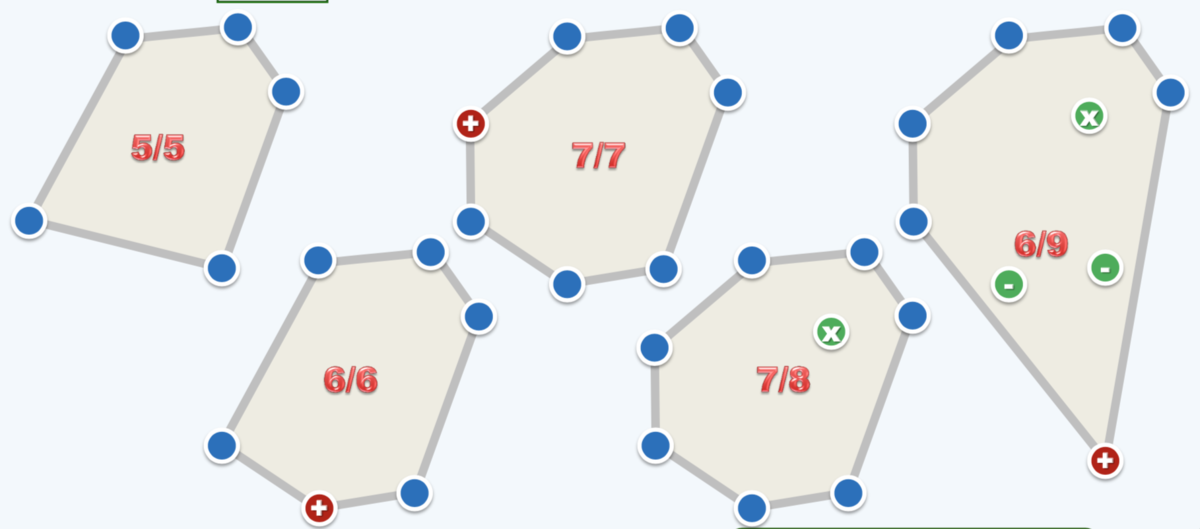
如上图,在添加新点时会发生三种情况:
- 该点作为新凸包上的点,且不影响原凸包上的点;
- 该点在目前凸多边形的内部;
- 该点作为新凸包上的点,并删除一些原凸包上的点。
那么怎么判断新加入的点属于上面哪种情况呢?我们一点一点看,先来判断新点是否属于原凸包内,也即判断点是否属于凸多边形的内部。
线性解法 —— 逆时针遍历凸多边形的所有边,执行 toLeft 判定。优势是可以应用于链表等动态内存结构,劣势是慢;
二分查找 —— 二分地判定点是否属于两条射线张成的区域之内,如下图。优势是快,劣势是只能应用于数组等静态内存结构。
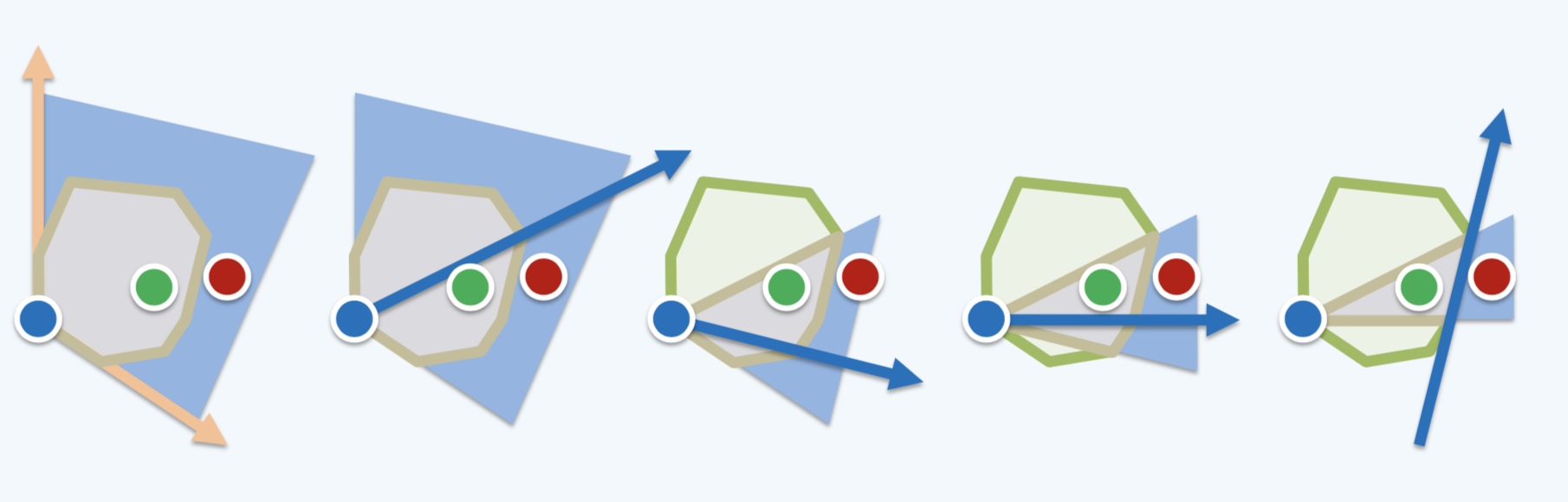
在增量法中,由于我们需要保证能够在常数时间内删除点,所以需要采用链表等结构,那么还是需要使用线性解法。
那么怎么应对刚刚说的第三种情况呢?我们将原凸包分成四部分:
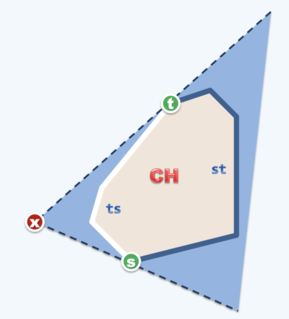
- 上、下切点();
- 段,需要被删除的部分;
- 段,需要保留的部分。
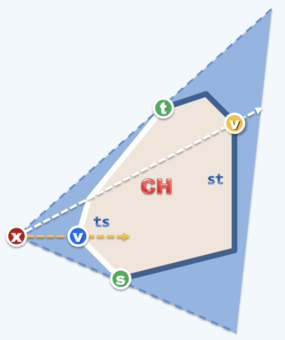
那么怎么判断点属于哪种类别呢?如上图,
- 若 的两个邻域点都分布在 的��左侧,则 是下切点;
- 若 的两个邻域点都分布在 的右侧,则 是上切点;
- 若 的两个邻域点(逆时针上、逆时针下)分布在 的左右侧,则 属于 段;
- 若 的两个邻域点(逆时针上、逆时针下)分布在 的右左侧,则 属于 段;
幸运的是,可以用类似的方法判断点是否在凸多边形内,也即判断其余点是否都属于 段。
Jarvis March
该算法的大致思想是逐条选出极边并加入到凸包中,如下图。
如下图,在算法运行中,怎样选取下个点,使得它与当前点 组成的边是下一条极边()呢?
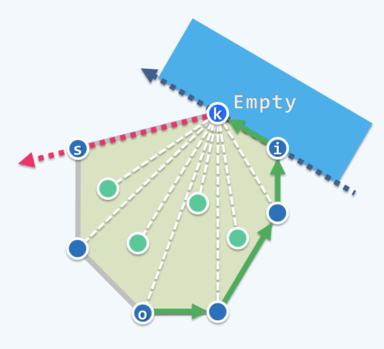
对于极点 ,只要找到点 ,使得 的右侧没有任何其他点。与本文一开始提出的第二个小问题类似,以 toLeft 测试为比较函数,找出其余点中最大的那个即可。
不失一般性,第一个极点 可以按照 lowest-than-leftmost 的规则选取。
凸包算法的下界
使用归约法(reduction)说明。关于归约法,维基百科有如下说明:
以直觉观之,如果存在能有效解决问题 B 的算法,也可以作为解决问题 A 的子程序,则将问题 A 称为“可归约”到问题 B,因此求解 A 并不会比求解 B 更困难。
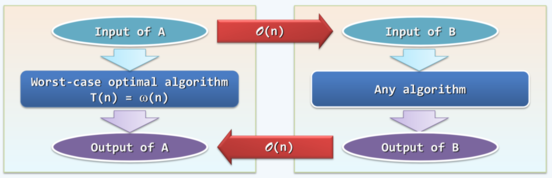
上图表示了一个线性�归约,如果对于问题 A 的任意输入都可以在线性时间内转换为某个 B 的输入,且对于问题 B 的输出都可以在线性时间内转换为 A 的输出,那么称问题 A 可以线性归约至问题 B。且问题 A 的下界也是问题 B 的下界。
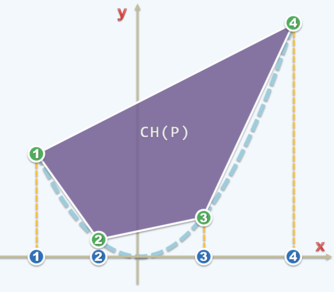
考虑基于比较的排序问题,对于一维上的所有输入,可以在线性时间内投影到抛物线 上。而投影过后的点集的凸包投影回一维上就是排序后的结果。则基于比较的排序问题可以线性归约为二维凸包问题,那么二维凸包问题的下界就是 。
下次将介绍几个 的凸包算法。